]

x = a:dx:b

the spacing is specified When element spacing dx is known.

x = linspace(a,b,n)

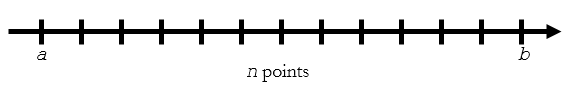the number of points is specified When number of elements n is known.

You can reshape any matrix into a column vector using x(:).

Concatenating Arrays

Horizontal Concatenation

horizontal concatenation using a space

Separate elements using a comma (,) or space ( )

Vertical Concatenation

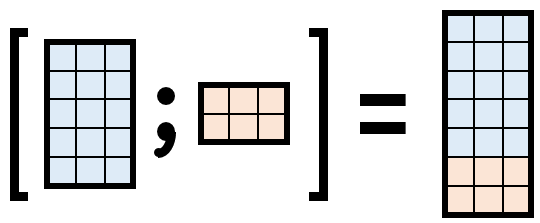
vertical concatenation using a semicolon

Separate elements using a semicolon (;)

Combined Concatenation

vertical and horizontal concatenation

Create each row separating elements with a comma (,) or space ( ), then separate the rows with a semicolon (;)

Array Creation Functions

Several functions exist that allow you to create arrays.

zeros ones rand randn eye magic compan gallery hadamard hankel hilb invhilb pascal rosser toeplitz vander wilkinson

For convenience, you can also leave one of the dimensions blank when calling reshape and that dimension will be calculated automatically.

y = reshape(x,5,[]);

If you want to remove elements from a vector, you can do so by assigning

v = [1 2 3 4 5];
v([2 4]) = []
    [1 3 5]

Summary: Accessing Data in Arrays

Indexing

column vector with 5 elements matrix with 5 rows and 4 columns

Extract one element from a vector

v(2)

1.5

Extract the last element from a vector

v(end)

1.3

Extract multiple elements from a vector

v([1 end-2:end])

When you are extracting elements of a matrix you need to provide two indices, the row and column numbers.

Extract one element from a matrix

M(2,3)

1.7

Extract an entire column. Here, it is the last one.

M(:,end)

Extract multiple elements from a matrix.

M([1 end],2)

      1.1
      2.8

Changing Elements in Arrays

Change one element from a vector

v(2) = 0

Change multiple element of a vector to the same value

v(1:3) = 0

Change multiple element of a vector to different values

v(1:3) = [3 5 7]

Assign a non-existent value

v(9) = 42

Remove elements from a vector

v(1:3) = []

Changing elements in matrices works the same way as with vectors, but you must specify both rows and columns.

Introduction to Matrix Multiplication

You have done element-wise arithmetic, including multiplication (.*). There is another way to multiply matrices, called matrix multiplication (*). It is the same matrix multiplication taught in linear algebra. You can think of it as a way to add elements in a row where you weight, or scale, the elements differently.

Weighted Sums

A weighted sum is where you scale numbers then add them together.

One example of this is how some teachers calculate final grades. If tests are worth 50% of the final grade, homework is 40%, and quizzes are 10%, then a student’s grades are calculated by multiplying these proportions by the test, homework, and quiz grades and adding them together.

Matrix-Vector Multiplication

Matrix multiplication of a matrix times a vector is the weighted sum of each row of the matrix.

So, imagine a teacher records the test, homework, and quiz scores of different students in the rows of a matrix. Multiplying the matrix of grades times the vector of weights, gives you the grades for each student.

Notice that the resulting matrix has the same number of rows as the matrix on the left — one final grade per student.

Matrix-Matrix Multiplication

When multiplying two matrices, the elements of the resutling matrix are the weighted sums of the rows and columns of the first and second matrix, respectively. Note that the matrix order is important since matrix multiplication is not commutative. That is,

AB≠BA

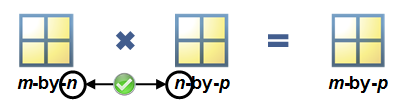
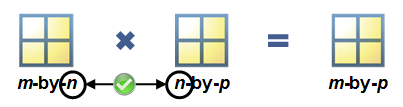
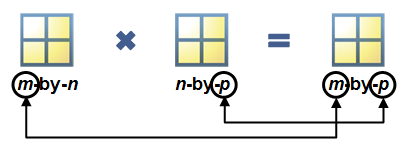
Matrix Dimensions

Matrix multiplication requires that the dimensions agree. You need the same number of columns in the first matrix as there are rows in the second, or there won’t be enough elements to multiply together.

Matrix multiplication requires that the inner dimensions of the two matrices agree. The resulting matrix has the outer dimensions of the two matrices.

x is a 2-by-3 matrix.

x = [1 0 7 ; 3 2 5]

x =

     1     0     7
     3     2     5

y is a 3-by-4 matrix.

y = [0 4 2 1 ; 2 1 0 2 ; 1 3 1 0]

y =

     0     4     2     1
     2     1     0     2
     1     3     1     0

The result z is a 2-by-4 matrix.

z = x*y

z =

     7    25     9     1
     9    29    11     7

Summary: Mathematical and Statistical Operations with Arrays

Performing Operations on Arrays

There are many operators that behave in element-wise manner, i.e., the operation is performed on each element of the array individually.

Mathematical Functions

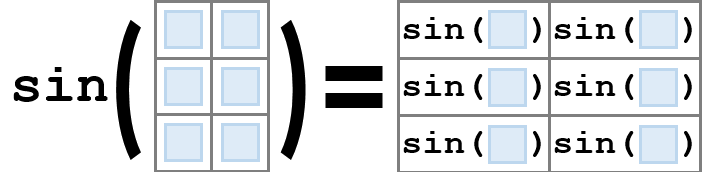
Other Similar Functions
`sin`	Sine
`cos`	Cosine
`log`	Logarithm
`round`	Rounding Operation
`sqrt`	Square Root
`mod`	Modulus
Many more

Matrix Operations (Including Scalar Expansion)

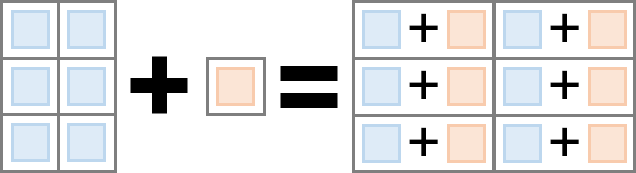
Operators
`+`	Addition
`-`	Subtraction
`*`	Multiplication
`/`	Division
`^`	Exponentiation (Matrix exponentiation)

Element-wise Operations

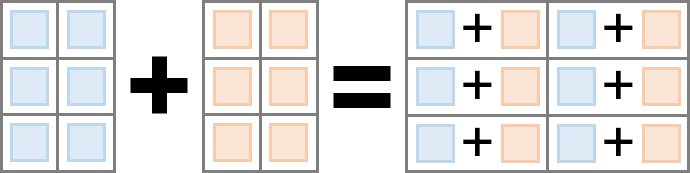
Operators
`+`	Addition
`-`	Subtraction
`.*`	Element-wise Multiplication
`./`	Element-wise Division
`.^`	Element-wise Exponentiation

Implicit Expansion

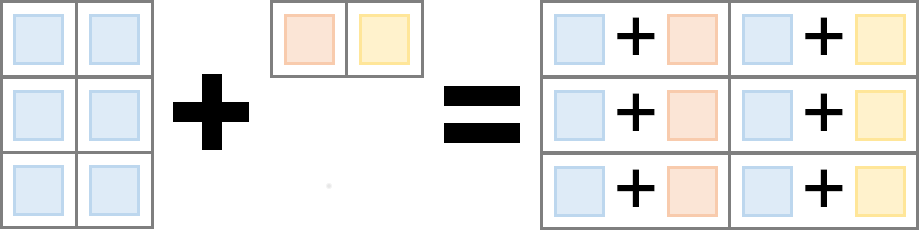
Operators
`+`	Addition
`-`	Subtraction
`.*`	Element-wise Multiplication
`./`	Element-wise Division
`.^`	Element-wise Exponentiation

Array operations can be performed on operands of different compatible sizes. Two arrays have compatible sizes if the size of each dimension is either the same or one.

Calculating Statistics of Vectors

Common Statistical Functions

Function	Description
`min`	Returns the minimum element
`max`	Returns the maximum element
`mean`	Returns the average of the elements
`median`	Returns the median value of the elements

Using `min` and `max`

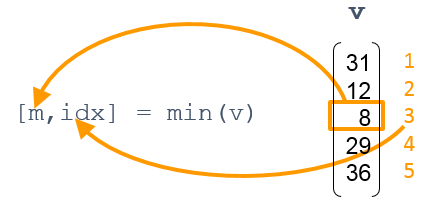
min with 2 outputs

Ignoring NaNs

When using statistical functions, you can ignore NaN values

  avg = mean(v,"omitnan")

Statistical Operations on Matrices

Some common mathematical functions which calculate a value for each column in a matrix include:

Function	Behavior
`max`	Largest elements
`min`	Smallest elements
`mean`	Average or mean value
`median`	Median value
`mode`	Most frequent values
`std`	Standard deviation
`var`	Variance
`sum`	Sum of elements
`prod`	Product of elements

		A = [8 2 4 ; 3 2 6 ; 7 5 3 ; 7 10 8] A = 8 2 4 3 2 6 7 5 3 7 10 8
		Amax = max(A) Amax = 8 10 8
		Astd = std(A) Astd = 2.2174 3.7749 2.2174
		Asum = sum(A) Asum = 25 19 21

Many statistical functions accept an optional dimensional argument that specifies whether the operation should be applied to columns independently (the default) or to rows.
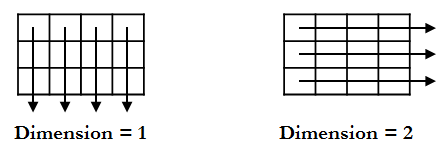
cols and rows

>>

 = mean(A,dim)

Outputs
`M`	Vector of average values along dimension `dim`.

Inputs
`A`	Matrix
`dim`	Dimension across which the mean is taken. `1`: the mean of each column `2`: the mean of each row

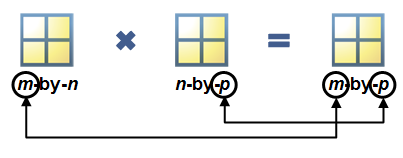
Matrix Multiplication

Matrix multiplication requires that the inner dimensions agree. The resultant matrix has the outer dimensions.

inner dimensions
outer dimensions

Solving Systems of Linear Equations

Expression	Interpretation
x = B/A	Solves `x*A=B` (for `x`)
x = A\B	Solves `A*x=B` (for `x`)

Summary: Tables of Data

Storing Data in a Table

The readtable function creates a table in MATLAB from a data file.

EPL = readtable("EPLresults.xlsx","TextType","string");

The table function can create a table from workspace variables.

teamWinsTable = table(team,wins)

teamWins =

           Team            Wins
    ___________________    ____

    "Arsenal"              20
    "Chelsea"              12
    "Leicester City"       23
    "Manchester United"    19

The array2table function can convert a numeric array to a table. The VariableNames property can be specified as a string array of names to include as variable names in the table.

stats = array2table(wdl, ...
    "VariableNames",["Wins" "Draws" "Losses"])

stats =

    Wins    Draws    Losses
    ____    _____    ______

    20      11        7
    12      14       12
    23      12        3
    19       9       10

Sorting Table Data

The sortrows function sorts the data in ascending order, by default.

EPL = sortrows(EPL,"HomeWins");

Use the optional "descend" parameter to sort the list in descending order.

EPL = sortrows(EPL,"HomeWins","descend");

You can also sort on multiple variables, in order, by specifying a string array of variable names.

EPL = sortrows(EPL,["HomeWins" "AwayWins"],"descend");

You can also show summary statistics for variables in a table.

summary(EPL)

Extracting Portions of a Table

Display the original table.

EPL

EPL =
           Team            HW    HD    HL    AW    AD    AL
    ___________________    __    __    __    __    __    __
    "Leicester City"       12    6      1    11    6      2
    "Arsenal"              12    4      3     8    7      4
    "Manchester City"      12    2      5     7    7      5
    "Manchester United"    12    5      2     7    4      8
    "Chelsea"               5    9      5     7    5      7
    "Bournemouth"           5    5      9     6    4      9
    "Aston Villa"           2    5     12     1    3     15

Inside parenthesis, specify the row numbers of the observations and column numbers of the table variables you would like to select.

EPL(2:4,[1 2 5])

ans =
           Team            HW    AW
    ___________________    __    __
    "Arsenal"              12    8
    "Manchester City"      12    7
    "Manchester United"    12    7

You may also use the name of the variable for indexing.

If you want to reference more than one variable, use a string array containing the variable names.

EPL(2:4,["Team" "HW" "AW"])

ans =
           Team            HW    AW
    ___________________    __    __
    "Arsenal"              12    8
    "Manchester City"      12    7
    "Manchester United"    12    7

Extracting Data from a Table

Display the original table.

EPL

EPL =
           Team            HW    HD    HL    AW    AD    AL
    ___________________    __    __    __    __    __    __
    "Leicester City"       12    6      1    11    6      2
    "Arsenal"              12    4      3     8    7      4
    "Manchester City"      12    2      5     7    7      5
    "Manchester United"    12    5      2     7    4      8

You can use dot notation to extract data for use in calculations or plotting.

tw = EPL.HW + EPL.AW

You can also use dot notation to create new variables in a table.

EPL.TW = EPL.HW + EPL.AW

EPL =
           Team            HW    HD    HL    AW    AD    AL    TW
    ___________________    __    __    __    __    __    __    __
    "Leicester City"       12    6      1    11    6      2    23
    "Arsenal"              12    4      3     8    7      4    20
    "Manchester City"      12    2      5     7    7      5    19
    "Manchester United"    12    5      2     7    4      8    19

If you want to extract multiple variables, you can do this using curly braces.

draws = EPL{:,["HD" "AD"]}

Specify row indices to extract specific rows.

draws13 = EPL{[1 3],["HD" "AD"]}

draws =
     6     6
     2     7

Exporting Tables

You can use the writetable function to create a file from a table.

   writetable(tableName,"myFile.txt","Delimiter","\t")

The file format is based on the file extension, such as .txt, .csv, or .xlsx, but you can also specify a delimiter.

writetable

Write a table to a file.

Summary: Organizing Tabular Data

Combining Tables

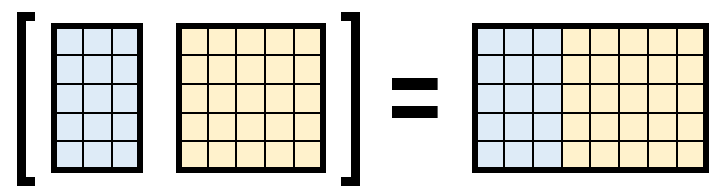
If the tables are already aligned so that the rows correspond to the same observation, you can concatenate them with square brackets.

[teamInfo games]

If the tables are not already aligned so that the rows correspond to the same observation, you can still combine the data by merging them with a join.

The join function can combine tables with a common variable.

top3 = join(uswntTop3,posTop3)

top3 =
Player          Goals          Position
    ___________________    ______    ___________________

    "Alex Morgan"           6        "forward"
    "Megan Rapinoe"         6        "forward"
    "Rose Lavelle"          3        "midfielder"

Table Properties

Display the table properties.

EPL.Properties

ans =
  Table Properties with properties:

             Description: ''
                UserData: []
          DimensionNames: {'Row'  'Variable'}
           VariableNames: {1×11 cell}
    VariableDescriptions: {1×11 cell}
           VariableUnits: {}
      VariableContinuity: []
                RowNames: {}
        CustomProperties: No custom properties are set.

You can access an individual property of Properties using dot notation.

EPL.Properties.VariableNames

ans =
  1×11 cell array
  Columns 1 through 4
    {'Team'}    {'HomeWins'}    {'HomeDraws'}    {'HomeLosses'}
  Columns 5 through 8
    {'HomeGF'}    {'HomeGA'}    {'AwayWins'}    {'AwayDraws'}
  Columns 9 through 11
    {'AwayLosses'}    {'AwayGF'}    {'AwayGA'}

Indexing into Cell Arrays

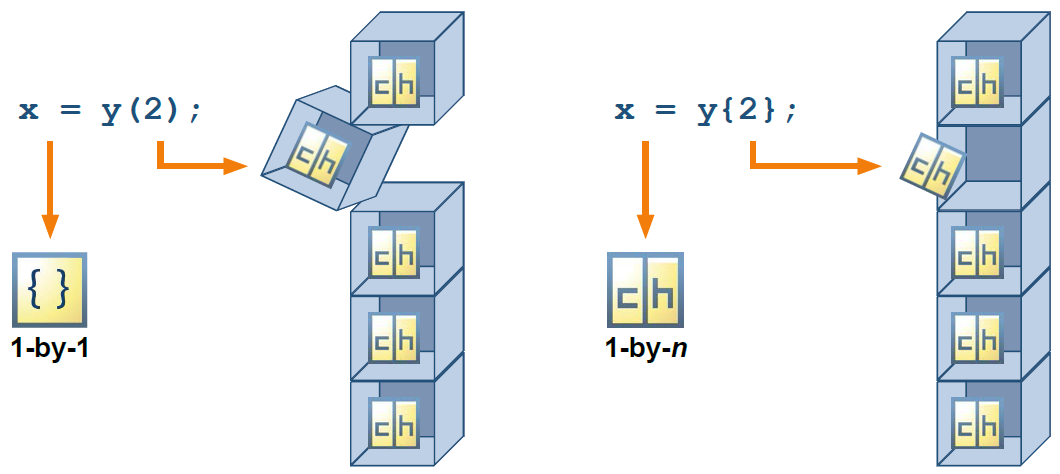
determining size

The variable varNames is a cell array that contains character arrays of different lengths in each cell.

varNames = teamInfo.Properties.VariableNames

'Team' 'Payroll_M__' 'Manager' 'ManagerHireDate'

Using parentheses to index produces a cell array, not the character array inside the cell.

varName(2)

'Payroll_M__'

In order to extract the contents inside the cell, you should index using curly braces, {}.

varName{2}

'Payroll_M__'

Using curly braces allows you to rename the variable.

varName{2} = 'Payroll'

'Team' 'Payroll' 'Manager' 'ManagerHireDate'

Summary: Specialized Data Types

Working with Dates and Times

Dates are often automatically detected and brought in as datetime arrays.

teamInfo

ans =
         Manager         ManagerHireDate
    _________________    _______________
    "Rafael Benítez"     3/11/2016
    "Claudio Ranieri"    7/13/2015
    "Ronald Koeman"      6/16/2014
    "David Unsworth"     5/12/2016
    "Slaven Bilić"       6/9/2015

Many functions operate on datetime arrays directly, such as sortrows.

sortrows(teamInfo,"ManagerHireDate")

ans =
         Manager         ManagerHireDate
    _________________    _______________
    "Ronald Koeman"      6/16/2014
    "Slaven Bilić"       6/9/2015
    "Claudio Ranieri"    7/13/2015
    "Rafael Benítez"     3/11/2016
    "David Unsworth"     5/12/2016

You can create a datetime array using numeric inputs. The first input is year, then month, then day.

t = datetime(1977,12,13)

t =
   13-Dec-1977

To create a vector, you can specify an array as input to the datetime function.

ts = datetime([1903;1969],[12;7],[17;20])

ts =
   17-Dec-1903
   20-Jul-1969

Operating on Dates and Times

Create datetime variables to work with.

seasonStart = datetime(2015,8,8)

seasonStart =
   08-Aug-2015

seasonEnd = datetime(2016,5,17)

seasonEnd =
   17-May-2016

Use subtraction to produce a duration variable.

seasonLength = seasonEnd - seasonStart

seasonLength =
   6792:00:00

Functions such as years and days can help make better sense of the output.

seasonLength = days(seasonLength)

seasonLength =
   283

They can also create durations from a numeric value.

seconds(5)

ans =
   5 seconds

Use the between function to produce a context-dependent calendarDuration variable.

seasonLength = between(seasonStart,seasonEnd)

seasonLength =
   9mo 9d

Create a calendar duration from a numeric input with functions such as calmonths and calyears.

calmonths(2)

ans =
   2mo

You can learn more about datetime and duration functions in the documentation.
Create Date and Time Arrays

Representing Discrete Categories

x is a string array.

x = ["C" "B" "C" "A" "B" "A" "C"];

x =
    "C"     "B"     "C"     "A"     "B"     "A"     "C"

You can convert x into a categorical array, y, using the categorical function.

y = categorical(x);

y =
    C     B     C     A     B     A     C

You can use == to create a logical array, and count elements using nnz.

nnz(x == "C")

ans =
        3

You can view category statistics using the summary function.

summary(y)

     A      B      C
     2      2      3

You can view combine categories using the mergecats function.

y = mergecats(y,["B" "C"],"D")

y =
     D      D      D      A      D      A      D

Summary: Preprocessing Data

Normalizing Data

normalize

Normalize data using a specified normalization method.

Normalize the columns of a matrix using z-scores.

xNorm = normalize(x)

Center the mean of the columns in a matrix on zero.

xNorm = normalize(x,"center","mean")

Scale the columns of a matrix by the first element of each column.

xNorm = normalize(x,"scale","first")

Stretch or compress the data in each column of a matrix into a specified interval.

xNorm = normalize(x,"range",[a b])

Working with Missing Data

Any calculation involving NaN results in NaN. There are three ways to work around this, each with advantages and disadvantages:

Ignore missing data when performing calculations.	Maintains the integrity of the data but can be difficult to implement for involved calculations.
Remove missing data.	Simple but, to keep observations aligned, must remove entire rows of the matrix where any data is missing, resulting in a loss of valid data.
Replace missing data.	Keeps the data aligned and makes further computation straightforward, but modifies the data to include values that were not actually measured or observed.

The Clean Missing Data task can be used to remove or interpolate missing data. You can add one to a script by selecting it from the Live Editor tab in the toolstrip.

Data contains missing values, in the form of both -999 and NaN.

x = [2 NaN 5 3 -999 4 NaN];

The ismissing function identifies only the NaN elements by default.

ismissing(x)

ans =
  1×7 logical array
   0   1   0   0   0   0   1

Specifying the set of missing values ensures that ismissing identifies all the missing elements.

ismissing(x,[-999,NaN])

ans =
  1×7 logical array
   0   1   0   0   1   0   1

Use the standardizeMissing function to convert all missing values to NaN.

xNaN = standardizeMissing(x,-999)

xNaN =
     2   NaN     5     3   NaN     4   NaN

Use the rmmissing function to remove missing values.

cleanX = rmmissing(xNaN)

cleanX =
     2   5     3     4

Ignores `NaN`s by default (default flag is `"omitnan"`)	Includes `NaN`s by default (default flag is `"includenan"`)
`max` `min`	`cov` `mean` `median` `std` `var`

Data Type	Meaning of “Missing”
`double` `single`	`NaN`
`string` array	Empty string (`<missing>`)
`datetime`	`NaT`
`duration` `calendarDuration`	`NaN`
`categorical`	`<undefined>`

Interpolating Missing Data

fillmissing

Fills missing values of an array or table.

Interpolation assuming equal spacing of observations.

z = fillmissing(y,"method")

Interpolation with given observation locations.

z = fillmissing(y,"method","SamplePoints",x)

Method	Meaning
`"next"`	The missing value is the same as the next nonmissing value in the data.
`"previous"`	The missing value is the same as the previous nonmissing value in the data.
`"nearest"`	The missing value is the same as the nearest (next or previous) nonmissing value in the data.
`"linear"`	The missing value is the linear interpolation (average) of the previous and next nonmissing values.
`"spline"`	Cubic spline interpolation matches the derivatives of the individual interpolants at the data points. This results in an interpolant that is smooth across the whole data set. However, this can also introduce spurious oscillations in the interpolant between data points.
`"pchip"`	The cubic Hermite interpolating polynomial method forces the interpolant to maintain the same monotonicity as the data. This prevents oscillation between data points.

Summary: Common Data Analysis Techniques

Moving Window Operations

The Smooth Data task can be used to smooth variation or noise in data. You can add one to a script by selecting it from the Live Editor tab in the toolstrip.

The Smooth Data task uses the smoothdata function.

Mean calculated with a centered moving k-point window.

z = smoothdata(y,"movmean",k)

Mean calculated with a moving window with kb points backward and kf points forward from the current point.

z = smoothdata(y,"movmean",[kb kf])

Median calculated with a centered moving k-point window.

z = smoothdata(y,"movmedian",k)

Median calculated with a centered moving k-point window using sample points defined in x.

z = smoothdata(y,"movmedian",k,"SamplePoints",x)

Linear Correlation

You can investigate relationships between variables visually and computationally:

Plot multiple series together. Use yyaxis to add another vertical axis to allow for different scales.
Plot variables against each other. Use plotmatrix to create an array of scatter plots.
Calculate linear correlation coefficients. Use corrcoef to calculate pairwise correlations.

Plot multiple series together.

yyaxis left
plot(...)
yyaxis right
plot(...)

Plot variables against each other.

plotmatrix(data)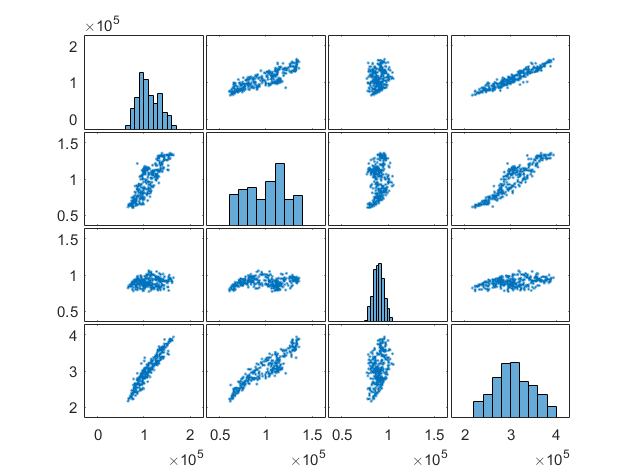

Calculate linear correlation coefficients.

corrcoef(data)

ans =
    1.0000    0.8243    0.1300    0.9519
    0.8243    1.0000    0.1590    0.9268
    0.1300    0.1590    1.0000    0.2938
    0.9519    0.9268    0.2938    1.0000

Polynomial Fitting

polyfit

Fits a polynomial to data.

polyval

Evaluates a polynomial at specified locations.

Simple fitting

Fit polynomial to data.

c = polyfit(x,y,n);

Evaluate fitted polynomial.

yfit = polyval(c,xfit);

Fitting with centering and scaling

Fit polynomial to data.

[c,~,scl] = polyfit(x,y,n);

Evaluate fitted polynomial.

yfit = polyval(c,xfit,[],scl);

Summary: Programming Constructs

User Interaction

You can add a live control to get input from the user.

You can use disp to show output on the command window.

disp("Message")

Message

You can use warning and error as well.

warning("Missing data")

Warning: Missing data

error("Missing data")

Missing data

The msgbox, errordlg, and warndlg functions can display messages to the user.

msgbox("Analysis complete")

Decision Branching

The condition_1 is evaluated as true or false.

if condition_1

If condition_1 is true, then the code_1 code block is executed.

    code_1

Otherwise, the next case is tested. There can be any number of cases.

elseif condition_2

    code_2

elseif condition_3

    code_3

If none of the cases are a match, then the code, code_e, in else is executed.

else
    code_e

Always end the expression with the keyword end

end

Evaluate expression to return a value.

switch expression

If expression equals value_1, then code_1 is executed. Otherwise, the next case is tested. There can be any number of cases.

    case value 1

        code_1

    case value 2

        code_2

If none of the cases are a match, then the code, code_3, in otherwise is executed. The otherwise block is optional.

    otherwise

        code_3

Always end the expression with the keyword end

end

Determining Size

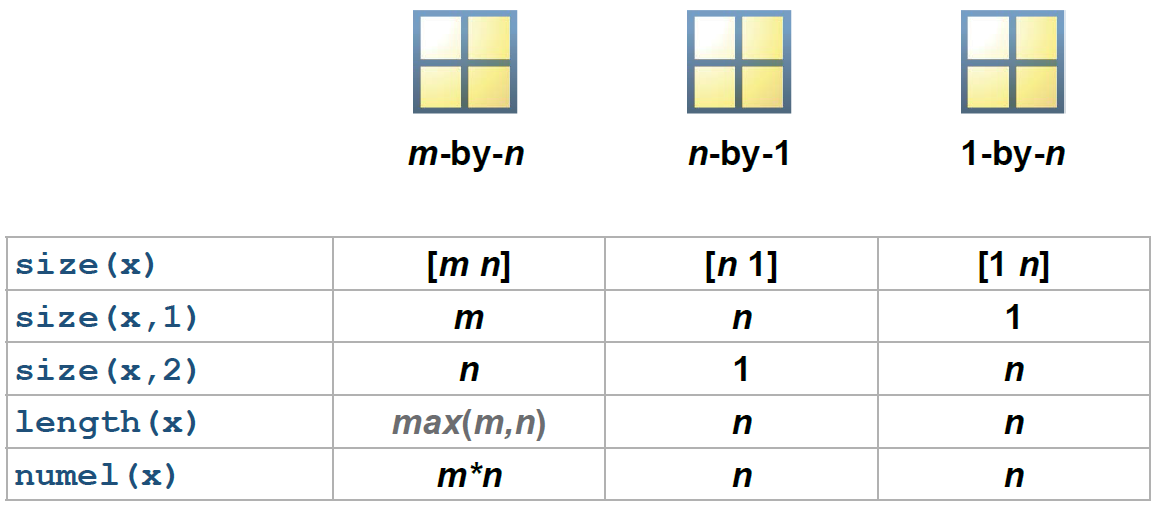
Use size to find the dimensions of a matrix.

s = size(prices)

s =
    19    10

[m,n] = size(prices)

m = size(prices,1)

m =
    19

n = size(prices,2)

n =
    10

Use length when working with vectors where one of the dimensions returned by size is 1.

m = length(Year)

m =
    19

Use numel to find the total number of elements in an array of any dimension.

N = numel(prices)

N =
   190

For Loops

The index is defined as a vector. Note the use of the colon syntax to define the values that the index will take.

for index = first:increment:last
    code
end

While Loops

The condition is a variable or expression that evaluates to true or false. While condition is true, code executes. Once condition becomes false, the loop ceases execution.

while condition
    code
end

Summary: Increasing Automation with Functions

Creating and Calling Functions

Define a function	Call a function

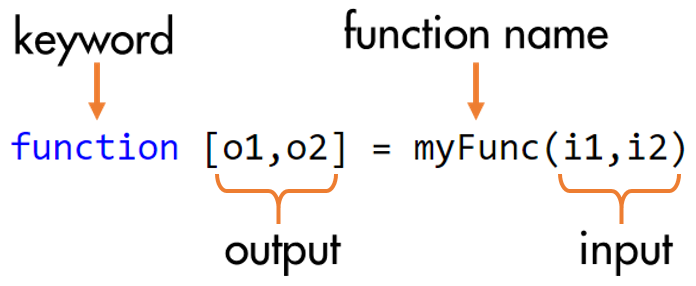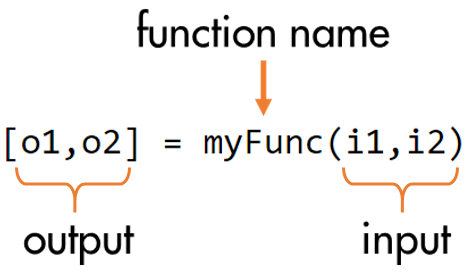Function Files

Function Type	Function Visibility
Local functions: Functions that are defined within a script.	Visible only within the file where they are defined.
Functions: Functions that are defined in separate files.	Visible to other script and function files.

Workspaces

A function maintains its own workspace to store variables created in the function body.

       a = 42;

b = foo(a);

foo.mlx

function y = foo(x)
a = sin(x);
x = x + 1;
b = sin(x);
y = a*b;
end

Base Workspace
a	42
b	0.7623

Function Workspace
a	-0.9165
b	-0.8318
x	43
y	0.7623

MATLAB Path and Calling Precedence

In MATLAB, there are rules for interpreting any named item. These rules are referred to as the function precedence order. Most of the common reference conflicts can be resolved using the following order:

Variables
Functions defined in the current script
Files in the current folder
Files on MATLAB search path

A more comprehensive list can be found here.

The search path, or path is a subset of all the folders in the file system. MATLAB can access all files in the folders on the search path.
To add folders to the search path:

On the Home tab, in the Environment section, click Set Path.
Add a single folder or a set of folders using the buttons highlighted below.

search path screenshot

Concatenating Arrays

Horizontal Concatenation

Vertical Concatenation

Combined Concatenation

Array Creation Functions

Summary: Accessing Data in Arrays

Indexing

Changing Elements in Arrays

Introduction to Matrix Multiplication

Weighted Sums

Matrix-Vector Multiplication

Matrix-Matrix Multiplication

Matrix Dimensions

Summary: Mathematical and Statistical Operations with Arrays

Performing Operations on Arrays

Mathematical Functions

Matrix Operations (Including Scalar Expansion)

Element-wise Operations

Implicit Expansion

Calculating Statistics of Vectors

Common Statistical Functions

Using min and max

Ignoring NaNs

Statistical Operations on Matrices

Matrix Multiplication

Solving Systems of Linear Equations

Summary: Tables of Data

Storing Data in a Table

Sorting Table Data

Extracting Portions of a Table

Extracting Data from a Table

Exporting Tables

Summary: Organizing Tabular Data

Combining Tables

Table Properties

Indexing into Cell Arrays

Summary: Specialized Data Types

Working with Dates and Times

Operating on Dates and Times

Representing Discrete Categories

Summary: Preprocessing Data

Normalizing Data

Working with Missing Data

Interpolating Missing Data

Summary: Common Data Analysis Techniques

Moving Window Operations

Linear Correlation

Polynomial Fitting

Simple fitting

Fitting with centering and scaling

Summary: Programming Constructs

User Interaction

Decision Branching

Determining Size

For Loops

While Loops

Summary: Increasing Automation with Functions

Creating and Calling Functions

Function Files

Workspaces

MATLAB Path and Calling Precedence

Using `min` and `max`